Mapping the Universe onto a Black Hole Interior

Hypothesis in Brief

1. The universe is a black hole interior.

2. Because all geodesics lead to the singularity, it would be perceived by an infalling observer as a bounding sphere.

3. Distant objects would recede due to increasing differential curvature along infalling paths.

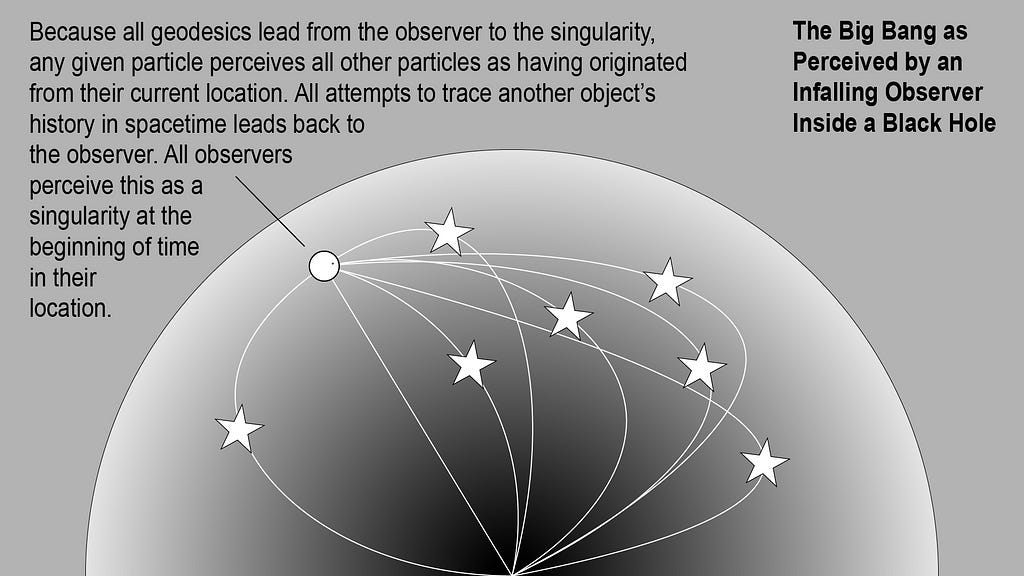
4. All geodesics lead from the observer to the singularity, causing the observer to assume all objects originate from their location, thus the appearance of a Big Bang.

5. As the observer adjusts to increasing curvature on their approach to the singularity, it would recede in space, giving the impression of an infinitely expanding bounding sphere.

Introduction

This essay aims to use Einstein’s theory of relativity to challenge popular notions about black holes. By exploring the unintuitive but logical implications of the Schwarzschild metric, I will demonstrate that our universe has strikingly similar characteristics to a black hole interior.

I’m not challenging any laws of physics here, nor will I contradict observational astronomy. We live in a homogeneous, isotropic, and infinitely expanding universe, and I don’t seek to challenge that.

I intend to complement, not contradict, this internal view of our universe with an external model.

My diagrams, while conceptually accurate, are extremely simplified so as to make unintuitive aspects of relativity more accessible.

Let’s explore how the perspective of an infalling object through a black hole interior maps onto our journey through the universe, from the Big Bang, to cosmic expansion, and finally to heat death.

(Note: I have recently argued (and am working on a mathematical proof to demonstrate) that time dilation is actually spatial expansion. I believe this to be the case, but for the sake of readability I’m going to follow current conventions throughout this essay.)

Hypothesis

To an observer falling through a black hole interior, the beginning of the journey at the event horizon is retroactively perceived as an expanding singularity (like the Big Bang). This is because all geodesics in a black hole lead back to the observer, so any attempt to trace the history of matter through spacetime leads to the conclusion of an expanding singularity at the beginning of time.

Similarly, but oppositely, the singularity at the center of the black hole is perceived as a sphere encompassing the black hole interior. The singularity manifests as a sphere because all geodesics in a black hole lead from the observer to the singularity. What the observer perceives as straight paths in space are actually geodesics bent toward the singularity. This causes the observer to perceive the singularity as an all-encompassing sphere.

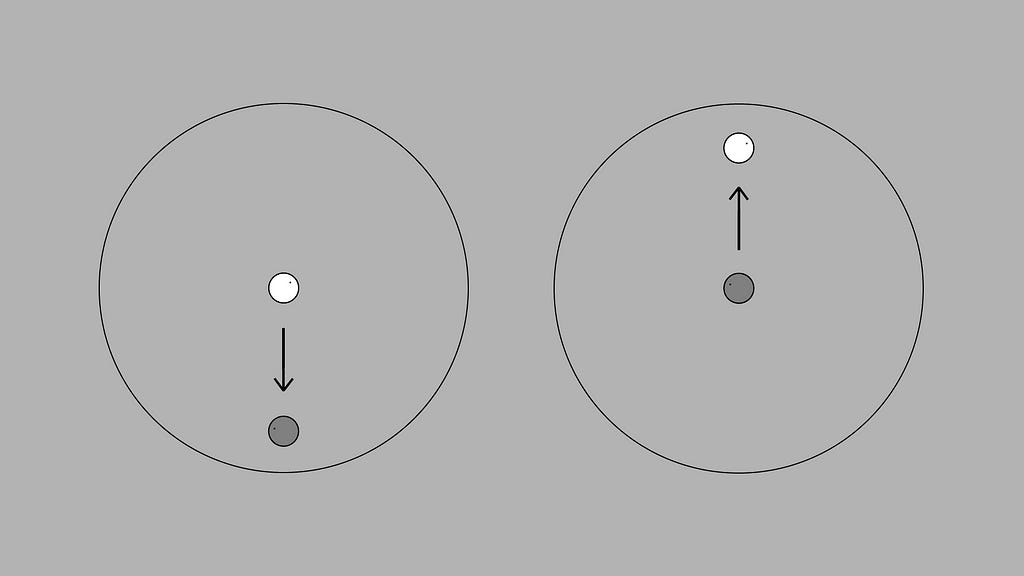
To get a better idea of this concept, take a look at this gravitational lensing diagram, which shows how a curved light path is perceived as straight by an observer.

Now let’s apply this concept to the extreme curvature of a singularity.

As the observer approaches the singularity, spacetime intervals between the observer and other infalling objects increase. The universally increasing curvature would lead to the perception of objects moving away with a rate proportional to distance. This accelerating universal geodesic lengthening is similar to what we observe in our expanding universe.

The singularity itself appears to move away in space as the observer falls toward it. This paradoxical effect is the result of increasing curvature along the observer’s infalling path. A simpler way to think of this is: as time runs out, space increases.

This effect is the result of the observer’s constant perception of local spacetime as flat. When curvature increases, spacetime intervals are increasingly perceived as spatial distances rather than time dilation in the observer’s frame.

In the observer’s perspective, this would manifest as an infinitely expanding bounding sphere that pulls everything else towards it.

Because spacetime in a black hole’s center is infinitely curved, it is possible for this curvature to be perceived as infinite space.

Another way to put this: from the outside, a black hole occupies fixed space but contains infinite gravity. On the inside, for an observer adjusting to that infinite curvature, gravity decreases and space increases in tandem until space appears infinite and observer-calculated density approaches zero.

To say it bluntly, I propose that an observer would perceive a black hole interior to be inside out — they’d place themselves at the center and see objects being driven away toward an infinitely expanding bounding sphere.

Foundational Concepts

The following definitions are grounded in relativity theory, but worded in a way that is nonstandard. The goal here is to deconstruct some of these concepts so we can draw unintuitive links between them.

My use of language that blurs traditional concepts is intentional, as I believe some of the established frameworks in relativity may stifle insight by being overly specific.

Spacetime

Physicists often refer to spacetime as the medium in which events take place in our universe. Other times it’s modeled as a two-dimensional fabric for the purpose of illustrating the effects of gravity on the passage of time.

This essay will occasionally make use of these metaphors, but keep in mind that spacetime is not literally a medium. When we say “space is expanding,” we really mean “distances between objects are universally increasing.”

The concept of expansion doesn’t explain why that’s happening, but sometimes the shorthand is so convenient we start thinking of it as a cause, which can lead to false assumptions and blind spots. Space itself can’t actually expand. Any claim that it does refers back to changes to paths through space–if space were totally empty, there would be no way to define its expansion.

My barebones definitions are as follows:

Space is any portion of the universe. Time is change in that space.

Infinity

Infinities don’t exist as physical realities in nature, but as limits.

For example, the energy required to accelerate an object to the speed of light is infinite. This is mathematically true, but it’s a description of the boundary of possibility rather than a situation that can actually happen.

Observer:

In physics, the term “observer frame” refers to how the universe exists from the perspective of a given point in spacetime.

The terminology is vulnerable to misinterpretation, because “observe” and “perceive” sound like the visual processing of a person. While a whole person can reasonably be called an observer in most situations, “observer” really refers to a single particle, and this distinction becomes important in extreme conditions.

So in physics, “observer perspective” doesn’t refer to what a person would visually see–it refers to how the entire universe actually exists in a given frame.

I use the word “actually” here carefully. Despite Einstein proving that all observer frames are equally valid and real, it’s tempting to think of individual observer perspectives as less real than an omniscient perspective outside the universe. This is understandable, but it’s flawed thinking, because really the opposite is true. The external perspective of the universe is the imaginary, theoretical frame, whereas a given observer perspective constitutes “actual” reality.

I’m hammering on this point because people, including me, have trouble grasping that multiple conflicting things can somehow all be actually happening, but this was one of Einstein’s great insights.

External versus observer frames:

The universe is defined as “all existing matter and energy.” This means that any external perspective is merely a map, and not a real or valid perspective, because there is nothing outside the universe.

For this essay, I’ve created diagrams that will clarify the logical steps that led me to my hypothesis. Each diagram will be labeled either as “observer perspective” or “external view.”

My goal is to show you how mathematically-derived external and infalling perspective view of a black hole align strikingly with the observationally-derived standard model of cosmology.

A theoretical connection is necessary, as it’s impossible to observe the inside of a black hole or the outside of our universe.

Relativity:

Einstein’s theory of relativity predicts that nothing can travel faster than light in any observer frame, and that light always travels at the same speed in all frames. The corollary to this speed limit of the universe is that all observers perceive the timing and location of events differently.

Compared to the rest of the universe, Earth is so small and low mass that observer frames in our day-to-day lives are nearly identical. If we regularly traveled to other galaxies or at significant fractions of lightspeed, humans would have a more intuitive understanding of relativity.

For example, every observer perceives themselves to be at rest in the center of their own frame. When astronomers study the universe, they find that we are at the center. Now imagine an observer frame at the very edge of the universe–in their frame, they’re at the center, and we’re not.

Relativity is how we describe the interactions between disparate observers who always exist at the center of the universe in their respective frames.

If you’re wondering what the universe would look like for an omniscient external observer who could reconcile all frames: a singularity, with every observer occupying the same point in spacetime.

Time dilation in general relativity:

(Note: As mentioned, I don’t believe time dilation is the correct interpretation of this phenomenon—it should be called spatial expansion for the reasons explained, but I’m going to use the conventional terminology here to bridge the gap between my theory and current thinking.)

Gravitational time dilation refers to the slower time passing of time in areas with greater gravitational field strength. Gravity curves spacetime, which means spacetime intervals increase proportional to gravitational field strength.

Time dilates, or passes more slowly, because light takes longer to travel the same spatial distance. The curvature means the geodesic, or path through spacetime, is now longer than the path through space.

I’m staying away from commonly-used phrases like “appears to pass more slowly” because, while it is true that an observer can visually perceive time dilation, the word “appears” makes it sound like an optical illusion.

The paradoxical truth is that time literally passes more slowly in stronger gravitational fields. This is true in observer frames, but, if you were to measure the passage of time on a local clock (what physicists call “proper time”), time would appear to pass normally because the clock itself ticks more slowly.

For the purpose of distinguishing between visual perceptions and observer realities, it’s important to understand that, in gravitational fields, spacetime curves and time slows proportionally to this curvature.

Geodesics:

A geodesic is a real or theoretical path following the curvature of spacetime. This is the path an object follows when influenced only by gravity.

This is always longer than the path “distance” through space alone — if we also account for time, including curvature due to gravity, we get the geodesic.

Observers perceive geodesics to be straight lines in their own frames.

Let’s look at our gravitational lensing diagram again, which shows how gravity bends the path of light through space.

In the observer view, we see a straight path between the observer and the star’s perceived location.

The bent light path in the external view shows us the curved path which would only be perceptible from another angle. What’s important to understand here is that if gravity curves geodesics, then straight lines perceived by an observer are not actually straight lines in spacetime. The stronger the gravitational field, the more curved the geodesics become.

If you’re wondering where the star “really” is in the observer’s frame, the safe answer is to say it’s behind the massive object as pictured in the external view on the right. That’s because if the observer could move out of the bent light path, they’d end up defining the gravitational lensing as a visual effect. But if the star appears to be in the same location regardless of the position of the observer, then where is it “really?”

To bring this back to the black hole proposal: if there’s no existing frame in which a black hole’s singularity can be perceived as anything other than a bounding sphere around the observer, then that’s what it really is.

The Local Perception of Flat Spacetime

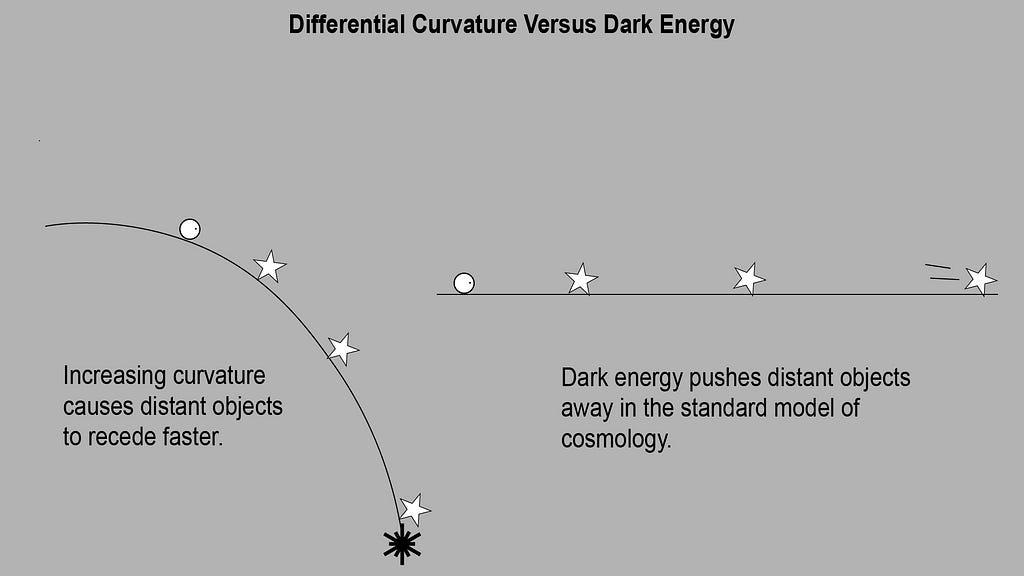
I propose that what we call “universal expansion” or “dark energy” is actually increasing spacetime curvature caused by falling toward the singularity of a black hole.

Spacetime graphs usually compare curved regions of spacetime to an idealized “flat spacetime” for an infinitely distant observer, which is how time passes in the total absence of gravity. However, in any given observer frame, local spacetime always appears to be flat.

The word “local” here is an approximation — it means that differential curvature isn’t causing significant changes to geodesics in the general vicinity of the observer. As conditions become more extreme, this area of estimated flatness shrinks in size.

Increasing spacetime curvature around an object lengthens the geodesic from the observer to the object. If the curvature could affect only the object, this would be perceived purely as time dilation. If the curvature could affect both the object and the observer equally, this would be perceived as pure motion away from the observer. In reality, it’s always a combination of the two.

Note that this perceived motion due to changing spacetime curvature is different from motion caused by a gravitational pull. Even if the object were somehow not attracted to the source of the gravity causing the spacetime curvature, it would still recede in the observer’s frame.

Differential Curvature and Universal Expansion

Because the observer perceives local spacetime to be flat, gravity and distance are constantly being exchanged as the observer adjusts to different curvature amounts.

I propose that the accelerating expansion of the universe is the result of an accelerating increase in non-uniform spacetime curvature.

This challenges the current explanation (a universal repulsive force termed dark energy), but it may align well with our observations of the expanding universe.

A black hole interior is the only model I can think of in which the universe can be pulled apart by its own gravity. Also note that, according to Einstein’s equivalence principle, the inhabitants of a black hole would not perceive their rapid infall. The only motion they’d be able to measure would be the differential acceleration between infalling objects.

So, to clarify, I’m not suggesting that distant galaxies are being pulled away to the singularity — my model proposes that all matter in the universe falls toward the singularity, but distant galaxies are being pulled faster than any given observer.

In our current understanding, all matter was aligned on the gravity axis at the beginning of time, occupying no space. At the end of time, all matter will be aligned on the space axis, with density approaching zero.

In both my model and the standard model, the universe functions like an hourglass that turns gravity into space via expansion. The mind-bending shape of a black hole interior, which allows infalling objects to appear to fall outwards, could accomplish this with its infinitely increasing spacetime curvature.

We can conceptualize the gravity-to-space exchange with the rotating spacetime axes of a given observer. As the axes rotate, gravity is increasingly exchanged for perceived space.

The concept of the tilting spacetime axes can also help us intuitively understand two pieces of my black hole hypothesis:

1. How we could be in an extremely strong gravitational field but not perceive the kind of time dilation we might expect heading toward a singularity, and

2. How the internal view of a black hole could feature infinitely expanding space while the theoretical external view would remain a fixed size at the Schwarzschild radius.

Spacetime Curvature Lengthens Geodesics

As I mentioned earlier, physicists often refer to groups of geodesics sitting in a spacetime medium.

By describing group operations to geodesics as changes to spacetime itself, our terminology can include information about why those changes are happening. This is often helpful, but it’s also misleading.

The following concepts are all different versions of the same thing: geodesics lengthening because of increasing spacetime curvature.

Expansion

The “metric expansion of space” is a cornerstone of the standard model of cosmology. It’s a conceptual description of what we observe in our universe: distant objects accelerate away from the observer at a rate proportional to distance.

Space as a medium is a useful concept for modeling geodesic paths, but it might be too useful. Stripped down to its core, space itself can’t be measured or even said to exist without geodesics. In attempting to solve these cosmological puzzles, I try to think strictly in terms of geodesics.

Dark Energy

Dark energy refers to the mysterious force that drives the expansion of the universe.

A placeholder concept can be a useful acknowledgement of an unsolved problem, but we can end up accepting it as an explanation even though we know it’s shorthand for an observed phenomenon.

Many (including me) have scratched their heads trying to answer the question “What is dark energy?”, when a better question would be “Why are geodesics between the observer and distant objects lengthening at a rate that accelerates proportional to distance from the observer?”

In my hypothesis, dark energy is not a repulsive force that drives distant objects away, but rather the result of spacetime curvature increasing inward from the singularity that we perceive as the edge of the universe. This increase in gravitational field strength happens everywhere, but not uniformly, so we perceive these lengthening geodesics as motion away from us.

Gravitational Time Dilation

“Time dilation” refers to the slower unfolding of events in a region of spacetime that is more curved than the observer’s location. It’s a relational concept — time passes more slowly, but more slowly than what? The answer is more slowly than it does in “flat” spacetime.

On the horizontal space axis, distance doesn’t change, so there’s no perception of motion. Instead, the geodesic dips down along the gravity axis. This means light traveling a given distance in that region must follow a longer geodesic than it would in the observer’s local spacetime, and therefore time dilates.

Redshifting

“Gravitational redshifting” describes the effect of time dilation on light wave frequency. When light travels through curved spacetime, its color shifts toward red. Observational astronomers can use the color offset to measure gravitational field strength and motion if they know what color a light source would be in flat (meaning local) spacetime.

Redshifting implies a lengthened geodesic, and as before, how much of the lengthening is interpreted as time dilation versus motion is dependent on the spacetime curvature at the observer compared to the redshifted object.

If a redshift is ascribed to motion rather than time dilation, it’s called “Doppler redshifting.” That’s when a light source is moving away from you in space and the perceived frequency drops proportionally to its relative speed.

I say “ascribed to” motion rather than “caused by” motion because, ultimately, redshifting is caused by a lengthening geodesic, and how much of that is gravitational versus doppler redshifting is defined by curvature at the observer’s location.

The geodesic change is more fundamental than whether an object moves or time dilates, so it’s more accurate to say that movement and time dilation are both caused by lengthening geodesics in curved spacetime.

Tidal Forces

As an observer and an object freefall through a strong gravitational field, they will drift apart because of differential acceleration — whichever object is closer to the source will accelerate faster.

In my model, differential acceleration is identical to universal expansion but on the scale of a single geodesic. The difference in spacetime curvature experienced by the observer and the object lengthens the geodesic between them.

In extreme environments such as the inside of a black hole, the difference in curvature would translate to drastic acceleration away from the observer, as well as significant time dilation.

Tidal Stretching

As spacetime curvature increases, the local region of perceived flatness around an observer shrinks progressively.

If the infalling object is larger than a single particle, eventually the curvature is so strong that different parts of the object undergo differential acceleration, or tidal stretching.

Again, tidal stretching aligns with my model of universal expansion in that it is caused by spacetime curvature increasing at different rates, but on a tiny scale.

These are all different ways to say “the geodesic got longer.”

Each of the above concepts describe a differential increase in spacetime curvature causing geodesics to lengthen.

I don’t mean to suggest these terms aren’t useful — they are, but it’s important to note that they are distinct only in how we perceive or group them. In an external view agnostic to gravity versus space, and only measuring the spacetime interval between two objects, they are all the same thing.

The Standard Model of Cosmology

The Friedmann-Lemaître-Robertson-Walker (FLRW) or standard model of cosmology is built on a foundation of math, observation, assumptions, and placeholder concepts.

While my hypothesis challenges some of the assumptions of the standard model, it may provide a more cohesive explanation of what we see: uniformity and isotropy, evidence of a Big Bang, and accelerating expansion.

This illustration shows cosmic expansion over the lifespan of the universe.

The universe appears to have begun with a period of rapid inflation originating at a single point in space, which we call the Big Bang.

After this inflationary epoch, the universe continued to expand gradually and at an accelerating rate. The acceleration of objects seems to be proportional to their distance from us, meaning more distant objects appear to recede faster.

I say “appear” here because what we actually measure, via various observational methods, is redshift, but we can’t say for sure what causes it. From the sole vantage point of our solar system, our ability to purely measure the spatial motion of distant galaxies is compromised. What we really measure is lengthening geodesics, but as we’ve discussed, the redshift we observe in distant galaxies could be the result of large-scale spacetime curvature, which would manifest as some combination of motion away from us and gravitational time dilation.

At this distance, it may not make much of a difference practically, but we may be limiting ourselves by assuming the redshift of distant galaxies is solely, or even mostly, due to motion in flat space. All we know for sure is that the geodesics are lengthening, but we don’t know why.

The standard model predicts that expansion will bring the universe to its end, either via a slow thermodynamic heat death or a “Big Rip” where expansion becomes so rapid that everything explodes. That would happen in a black hole, too.

Unexplained Expansion: Dark Energy, the Cosmological Constant, and the Hubble Constant

Coined in 1998, dark energy is conceptualized as a mysterious repulsive force that accelerates objects away from us. This is a placeholder explanation for Edwin Hubble’s 1929 discovery that distant galaxies accelerate away from us more quickly.

Dark energy is sometimes framed as an intrinsic quality of space itself, but mathematical representations of dark energy such as the cosmological constant Λ and the Hubble parameter (H₀) are observationally derived and need to be updated every decade or so as new data is obtained.

I propose that dark energy is simply gravity, and that what looks like outward expansion is instead objects experiencing differential spacetime curvature as they fall toward the spherical encompassing singularity of our black hole. The expansion would be a function of the universe’s geometry rather than an unexplained force.

Black Hole Anatomy

Can true black holes exist?

As far as I can tell, there isn’t a scientific consensus as to whether a true black hole can exist in our universe.

In 1939 Einstein and Oppenheimer both argued that singularities can’t form in finite time for any external observer, and Roy Kerr published a paper in December 2023 in which he claimed the belief that black holes contain singularities is unfounded.

True black holes are presented as real in current textbooks, but I spoke to several physicists during my research for this essay, and they had a wide variety of opinions on the topic. One black hole expert was so skeptical of true black holes he scoffed at the idea that anyone would believe they can exist.

I’ll be writing a follow-up piece about logical fallacies around black holes, because I hear a lot of contradictory axioms being invoked whenever they’re brought up. But briefly, my position is that the astronomical objects we call black holes are approaching the formation of a true event horizon but will never get there.

It may sound contradictory to say I don’t believe in black holes and yet I think we are in one, but the issue is that spacetime is so curved around a black hole that time dilation at the event horizon is infinite — meaning time slows to a stop for any outside observer. The paradox is that the process by which that event horizon forms would also take infinite time in any external frame.

So if you believe the event horizon experiences infinite time dilation (and by definition it does), then you should also believe it can never finish forming unless you are there.

The only way an event horizon can exist is if you’re inside it already.

For the purpose of this essay, “black hole” refers to the theoretical object described by Schwarzschild’s solution to Einstein’s field equations, not the objects we observe in the universe.

What’s a black hole?

A black hole is a region of spacetime so dense that nothing can escape. Once a mass is compressed into a small enough radius, called the Schwarzschild radius, gravitational collapse ensues and the spacetime inside becomes so curved that not even light can escape.

Physicists maintain that general relativity breaks down as you near a singularity, but I’m endeavoring to hang on to relativity until the bitter end. What follows is my attempt to follow logical steps within the framework of relativity but beyond current scientific consensus.

The Event Horizon and “Proper Time”

The event horizon forms at the Schwarzschild radius of the black hole, and is named such because events on one side cannot affect events on the other.

Time dilation, or gravitational redshifting, at the event horizon is infinite. Paths through spacetime are infinitely long as you approach this boundary, which means even light has to travel infinitely far to cross it.

If we remember that time dilation and space both represent geodesic length, you can see why I don’t believe anything could enter an event horizon in any observer frame.

It’s a well known axiom in astrophysics that an observer wouldn’t notice anything in particular if they fell into a black hole, but this perception is an artifact of how proper time is calculated. The infinite curve representing time dilation is integrated, meaning it’s mathematically divided into finite sections that translate into infinitely slowing proper time for the infalling observer.

This mathematical reconciliation is designed to get the local speed of light in space back up to c, but the problem (which I described in my last essay) is that it appears to increase the speed of light along a geodesic above c in the observer’s frame. This can’t happen — the speed of light across spacetime is always c in all frames.

Tilting the space axis to reflect the observer’s new sense of flat spacetime fixes this, and this means that lengthened geodesics in space time, what we call time dilation, is actually always spatial expansion.

I say “actually” here because it’s true in all frames. The expanded space may not be perceptible to a distant observer, and would indeed mimic time dilation in weaker gravitational fields (such as flying an atomic clock around the world in an airplane), but in stronger fields the lengthened spatial distances would begin to distort and rip apart objects that now occupy huge swaths of expanded spacetime.

Another consequence of infinite time dilation at an event horizon is that all infalling matter must arrive simultaneously and any outside universe must also not exist. Asking where the infalling matter came from is not a meaningful question because there’s definitionally nothing outside.

You are probably wondering where everything came from, and so am I, but the definition of “from” in a black hole is “further from the singularity.” At the event horizon, there is no “from,” so, as illogical as it sounds, the conclusion here is that the infalling matter in our black hole didn’t come from anywhere.

I will speculate a bit further about this at the end of the essay, but for our purposes we’ve hit the edge of causality and meaning.

Singularity

The singularity at the center of a black hole has a fixed mass, but this mass is compressed down to a single point in spacetime, causing infinite density, gravity, and curvature.

Infinite curvature is another way of saying that as geodesics near the singularity, they are increasingly bent towards it, so all spacetime paths terminate at the singularity.

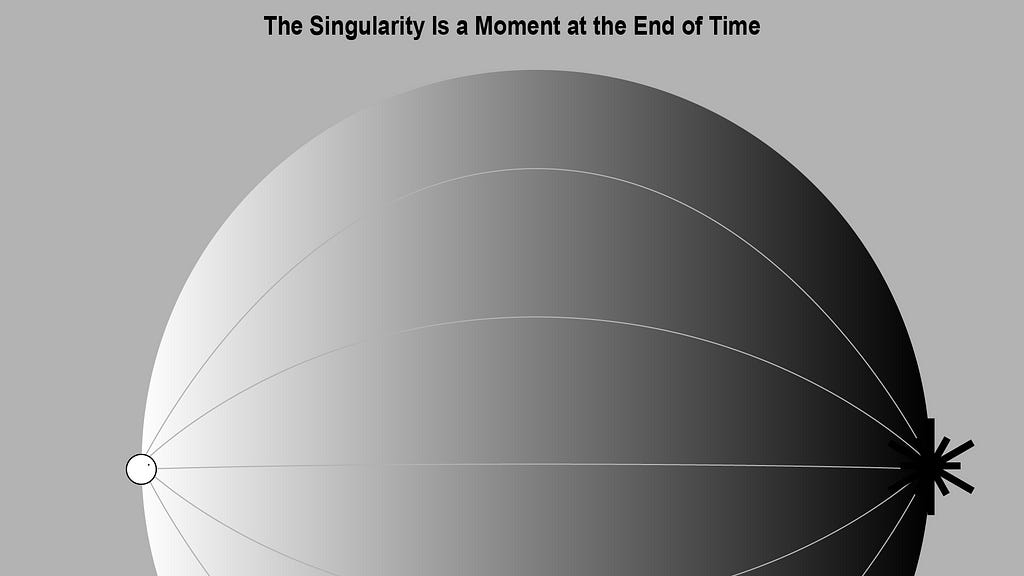
Confusingly, the singularity is essentially the black hole itself, but in a space/time swapped state at the end of time. Because it’s the end, it actually doesn’t physically exist within the temporal bounds of the black hole, just like the event horizon.

Since all matter is destined to end up at the singularity, it’s no longer meaningful to define it as a “place” as distinct from the rest of the black hole, since all possible markers are infalling as well, so the fall is perceived entirely as movement through time. The singularity is an event that marks the end of time for the infalling observer.

I understand my proposal that we perceive the singularity as a sphere is highly unintuitive and confusing.

You may be thinking, “If I were in a black hole, why couldn’t I look away from the singularity? I can look wherever I damn well please.”

You can’t. The geodesic from your retina to your pupil can’t point away from the singularity, no matter how you turn your head. This makes it impossible to perceive the singularity as having any specific location, making it omnidirectional, or a sphere.

This is confusing, but remember the gravitational lensing diagram. What you perceive as straight lines in space could be a completely different shape in spacetime, and you’d have no idea.

Trying to look backwards in a black hole is like trying to look behind you in time. It’s definitionally no longer a spatial direction.

Your possible next thought: “If I eat a pretzel, when I bring it towards me, isn’t it getting further away from the singularity if it’s a bounding sphere?”

No, but for two reasons that are hard to conceptualize simultaneously.

Imagine you are on a plane to Hawaii and you take a bite of your pretzel. The pretzel’s trip to your mouth is still on a forward trajectory due to the plane’s speed. So while things can freely move toward you, they are still also traveling with you to the singularity.

If you accept the relative speed part, the other confusing part is the singularity’s apparent motion away from you. That’s the result of you entering regions of ever increasing curvature and perceiving spatial expansion. On your geodesic, you’re getting closer, but as you continuously adjust to the increasing curvature, spatial distance is increasing.

Therefore the singularity is perceived — and could validly be defined as — an infinitely receding sphere surrounding a black hole interior.

Time and Space Swap Roles

Physicists sometimes say that time and space in a black hole “swap roles.” This is often presented as a metaphorical shorthand, but I argue that it’s literally true.

An observer’s space and gravity (or time dilation) axes rotate ninety degrees upon entry into a black hole. Then, over the course of infall, they rotate another ninety degrees.

This means that the spacetime curvature caused by infinite gravity flattens out over time, causing expanding space.

In fact, in my model, the passing of time itself can be defined as the observer moving into an increasingly strong gravitational field. While you can locally move between fields of different strengths, since everything is always falling toward the singularity, gravitational field strength is always increasing for the observer.

That is, time is always passing, and the only way to outrun it would be to travel faster than the speed of light (which is also the speed of gravitational wave propagation).

Spaghettification

You can probably tell I’m critical of certain physics terminology, but this one is a keeper.

It’s caused by differential acceleration in extreme curvature, and the word is so good that it needs no further explanation.

Comparing a Black Hole Interior to Our Universe

Okay, let’s map what we’ve established about black holes onto the standard model of cosmology.

The Big Bang

If we were in a black hole, and all matter falls along geodesics leading from the observer to the singularity, then any attempt to trace the history of matter in spacetime would cause the observer to conclude that they are at the center of a universe that expanded from a single point in spacetime.

So, in my argument, did the Big Bang “really” happen? Yes.

At the beginning of time, infalling matter is arranged in a sphere at the event horizon. But the pull of the singularity is so strong that radial movement is impossible. This means that each observer is definitionally at the furthest point from the singularity, which in turn, very confusingly, means they are already all in the same place even though they’re arranged in a sphere.

Two other ways to wrap your head around this:

1. Theoretically stepping outside the universe means swapping space and time, so it turns the diagram inside out. The sphere becomes a point and the point becomes a sphere. You may be tearing your hair out trying to figure out how these things are “actually” both happening, but they’re not. The universe is real, and a black hole is a mathematical map that explains the universe. So you’re doing the equivalent of trying to figure out how a drawing of Oregon can be the same as Oregon — it’s just not.

2. On the other hand… the only particle that can travel radially in a black hole is one with a lightlike path, such as a photon. Photons follow null geodesics with zero length. So, mathematically, a sphere around the event horizon at any radius translates to a single point in space in our universe. This means that space in the black hole is one-dimensional, just like time is in the universe.

To really stretch our brains, we can say the inverse is true: time (or gravity) in a black hole is three dimensional, like space is in a universe. Although the observer’s infalling spatial path ends up being a straight line along which all infalling matter travels, the observer is free to rotate that line around the singularity with lateral movement.

A light cone represents all the possible spacetime one could traverse if one were a photon, and is a way to visualize the boundaries of your future in spacetime.

In our universe, one can move in three dimensions in space but we’re pulled inexorably forward through time. In the black hole map, a light cone would show that the observer can move freely through time but is pulled inexorably forward through space.

Expansion, Dark Energy, and Spacetime Curvature

Gravity and curvature are the same thing. There’s no flat gravitational force. For example, if you hollowed out a giant ball of steel with the weight of a million suns, it would rip you apart to be anywhere near the outside, but on the inside would be zero gravity and zero time dilation inside.

For a gravitationally bound system such as the Milky Way galaxy, the effects of increasing curvature are minimal at the moment. By contrast, other galaxies are traveling away from us extremely quickly, because even though the differential acceleration is slight, it’s also cumulative, and there’s nothing to meaningfully slow them down.

You can see here how the effects of infinitely increasing curvature would closely mimic the universal expansion we observe.

Heat Death/The Big Rip

The current thinking is that the likely fate of our universe is heat death: entropy approaches infinity, density and temperature approach zero, and time effectively stops because no more events can occur.

The big rip is the same scenario, except universal expansion increases to a rate where galaxies, solar systems, planets, and objects in general are torn apart.

I believe a big rip is a likely scenario, which of course maps neatly onto the spaghettification concept. Some more physics-educated readers might point out that spaghettification only involves stretching along one dimension — the infalling path — but remember that a one dimensional path in a black hole maps onto three dimensional space in the universe.

(The mapping of one dimension onto three suggests that particle behavior in one frame would be wave-like in the other, and vice versa.)

A Not So Final Thought

Near the end of an observer particle’s fall into the gravity well of a singularity, the observer experiences extreme spatial expansion and isolation — remember the tilting spatial x-axis and how it exchanges gravity for time.

But — does a single observer particle really have an x-axis? Does it make any distinction between expansion and gravity, timelines and spacelines, or beginnings and endings?

Perhaps these concepts only apply to relationships between particles.

It’s possible that particle interactions are the building blocks of the universe more than particles themselves.

Or maybe the end of the universe is really is asymptotic heat death and isolation for every particle, until they can no longer be defined as existing.

The truth is, I have no idea what happens in the singularity.